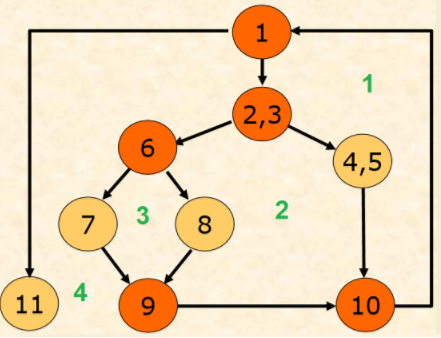
Thay vì dùng số nút và cạnh để tính độ phức tạp chu trình, hãy đếm số miền bị chia ra
1. Đồ thị dòng và cách xác định¶
Đồ thị dòng là một kỹ thuật dựa trên cấu trúc điều khiển của chương trình. Nó khá giống đồ thị luồng điều khiển của chương trình.
Chúng ta xây dựng đồ thị luông điều khiển của trương trình từ việc phân tích source code.
Ví dụ: Đồ thị luông điều khiển của trương trình có dạng như hình dưới.
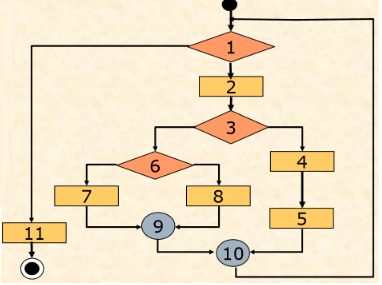
Từ đồ thị luồng điều khiển, chúng ta thu được đồ thị dòng bằng cách:
- Gộp các lệnh tuần tự , có nghĩa là gộp các nút mà từ nút này luôn đi qua nút kia.
- Thay lệnh rẽ nhánh và điểm kết thúc của các đường điều khiển bằng 1 nút vị tự
Ví dụ chúng ta xét luôn ví dụ từ đồ thị luồng ở trên:
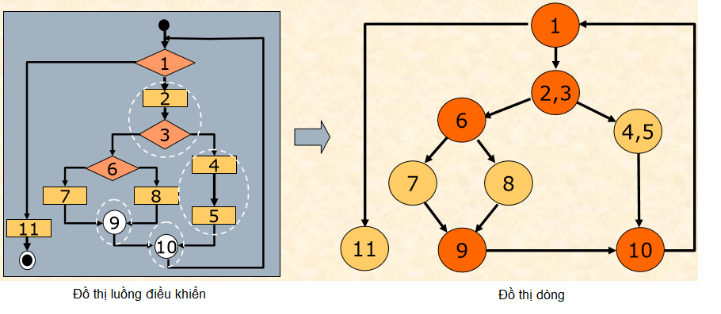
Ở ví dụ trên, ta thấy nút 2 và 3 có thể ghép được với nhau vì dòng chảy từ 2 luôn luôn đi qua 3, tương tự cho nút 4 và 5, và cũng tương tự cho nút 9 và 10
Sau khi biến đổi từ đồ thị luồng điều khiển, đồ thị dòng có cấu trúc:
- Mỗi nút (hình tròn) biểu thị một hay một số lệnh tuần tự, hoặc thay cho điểm hội tụ các đường điều khiển.
- Mỗi cạnh nối hai nút biểu diễn dòng điều khiển
](https://kipalog.kaopiz.com/uploads/9831/9924/image.png)
Từ đó ta thu được các thông số như sau:
- 9 nút (trongđó 5 nút là vị tự (mầuđỏ) - Xin nhắc lại: nút vị tự là nút rẽ nhánh hoặc nút kết thúc rẽ nhánh)
- 11 cung
- Chia mặt phẳng thành 4 miền (Số miền được xác định như hình trên, phần đánh số màu xanh lá cây)
2. Độ phức tạp Cyclomatic¶
Từ các thông số ở trên, chúng ta tính toán độ phức tạp của đồ thị, việc tính này cho phép mình biết được chính xác có bao nhiêu đường dẫn cơ sở.
Độ phức tạp (ký hiệu V(G) ) được tính theo một trong các công thức sau:
- V(G) = E - N + 2 (= 11-9+2 = 4)
- V(G) = số miền phẳng (= 4)
- V(G) = P – 1 (= 5-1 =4)
Trong đó: E=số cung; N=số nút; P=số nút vị từ
Với ví dụ về đồ thị dòng ở trên ta có: V(G) = 4